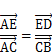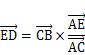NOI 2009 描边

问题简述

平面上有一些笔画，笔画两端为半圆，中部为矩形，笔画可以互相重叠。任务是求平面上笔画的总面积。

问题建模

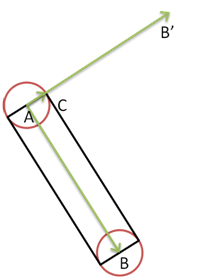
这是一个计算几何问题，我们可以把一个笔画分解看为一个矩形和两个圆相互重叠（如下图所示）。

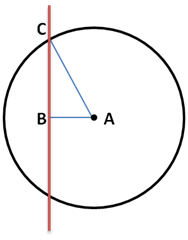
由于题中给定的是笔画的两个端点的坐标和半径，所以首先要求出矩形的四个端点坐标。如下图所示，设矩形两端中点分别为A,B，矩形A所在边上一个顶点为C。只需求出的长度相等的平面法向量，然后除以求出单位向量，再乘以R就能求出。用A,B坐标分别加减，即可求出矩形四个顶点的坐标。

解法竖线扫描

算法描述

用一条竖线去切割平面，会与上面的矩形或圆相交而且有一些相交的区间，把这些区间求并以后并乘以竖线的宽度，即可近似认为是竖线覆盖到的图形面积。用竖线扫描完整个平面，其面积之和就是平面上图形面积。扫描的竖线越细，结果就越精确。

我们要解决竖线与线段相交，以及竖线与圆相交的问题。

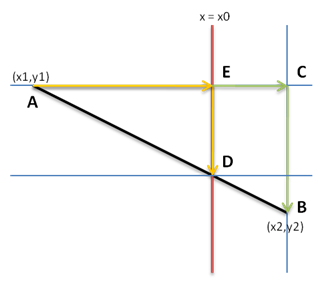
如图所示，扫描线x=x0与线段AB相交，我们要求出交点D的纵坐标。分别过B作平行于x=x0的直线，过A作垂直于x=x0的直线，相交于点C，AC交x=x0与点E。显然有

所以

于是用E的坐标加上可算出D坐标。

如图是扫描线与圆A相交点C，作AB垂直于扫描线与点B，连接AC。|AC|=R，|AB|为扫描线横坐标与点A横坐标之差绝对值，根据勾股定理即可求出|BC|，进而求出扫描线与圆的两交点坐标。

在程序实现时，我们需要求出每个“笔画”的左右边界横坐标，按照左边界坐标排序所有“笔画”，并用一个双向链表实现队列维护当前扫描线可以扫描到的“笔画”。扫描线向右移动时，判断是否有新的“笔画”左界小于等于扫描线横坐标，并加入队列。同时，当发现一个“笔画”右界小于扫描线横坐标，则把它从队列中删除。

实际测试

时间复杂度为O(MC)，M为笔画数，C为扫描线数。在实际的测试中，前9个测试点扫描竖线宽度设定为1*10^(-6)，均得到了10分，程序运行时间如下表。

测试点	1	2	3	4	5	6	7	8	9
时间(秒)	10	10	34	25	50	27	10	17	335

而第10个测试点由于规模过大，运行400秒仅能得到7分。当我把扫描竖线宽度设定为5*10^(-8)，，并运行了11天零4个小时后，终于获得了10分。

```cpp /* * Problem: NOI2009 path * Author: Guo Jiabao * Time: 2009.10.9 13:50 * State: Solved * Memo: 竖线扫描 */ #include #include #include #include #include #include using namespace std; const int MAXN = 2501; const double INF = 1e100;

struct point { double x,y; point (double tx,double ty) : x(tx),y(ty) {} point () : x(0) , y(0) {} };

struct shape { point c[2],v[4]; double left,right; };

struct itvs { double a; bool s; }isl[MAXN];

struct delist { struct item { item *c[2]; shape *e; item(item *last,shape *te) { c[0] = last; c[1] = NULL; e = te; } }*front,*rear; delist() { front = rear = 0; } void insert(shape *e) { if (rear) rear = rear -> c[1] = new item(rear,e); else front = rear = new item(NULL,e); } void remove(item *i) { if (i -> c[0]) i -> c[0] -> c[1] = i -> c[1]; else front = i -> c[1]; if (i -> c[1]) i -> c[1] -> c[0] = i -> c[0]; else rear = i -> c[0]; delete i; } };

int M,N,ic; double R,Total,Left,Right,miny,maxy; point P[MAXN]; shape A[MAXN]; delist DL;

void operator *= (point &a,double k) { a.x *=k; a.y *=k; }

point operator + (point a,point b) { return point(a.x + b.x,a.y + b.y); }

point operator - (point a,point b) { return point(a.x - b.x,a.y - b.y); }

inline double MIN(double a,double b) { return a<b?a:b; }

inline double MAX(double a,double b) { return a>b?a:b; }

inline double ABS(double a) { return a<0?-a:a; }

inline double dist(point a,point b) { return sqrt((a.x-b.x)(a.x-b.x) + (a.y-b.y)(a.y-b.y)); }

void init() { int i,a,b; freopen(“path.in”,“r”,stdin); freopen(“path.out”,“w”,stdout); scanf("%d",&N); for (i=1;i<=N;i++) scanf("%lf%lf",&P[i].x,&P[i].y); scanf("%d",&M); for (i=1;i<=M;i++) { scanf("%d%d",&a,&b); A[i].c[0] = P[a]; A[i].c[1] = P[b]; } scanf("%lf",&R); }

void count_point() { int i; point v,v1,v2; Left = INF; Right = -INF; for (i=1;i<=M;i++) { v = A[i].c[1] - A[i].c[0]; v1.x = v.y; v1.y = -v.x; v1 *= R / dist(A[i].c[0],A[i].c[1]); A[i].v[0] = A[i].c[0] + v1; A[i].v[1] = A[i].c[0] - v1; A[i].v[2] = A[i].c[1] + v1; A[i].v[3] = A[i].c[1] - v1;

    A[i].left = MIN(A[i].c[0].x-R,A[i].c[1].x-R);
    if (A[i].left < Left)
        Left = A[i].left;
    
    A[i].right = MAX(A[i].c[0].x+R,A[i].c[1].x+R);
    if (A[i].right > Right)
        Right = A[i].right;
}

}

inline int cmp(const void *a,const void *b) { return ((shape *)a) -> left < ((shape *)b) -> left ? -1 : 1; }

inline int cmp1(const void *a,const void *b) { if ( ((itvs *)a) -> a < ((itvs *)b) -> a ) return -1; else if ( ((itvs *)a) -> a > ((itvs *)b) -> a ) return 1; if (((itvs *)a) -> s) return -1; return 1; }

void insert_ivl(double s,double t) { if (s >= t) return; isl[++ic].a = s; isl[ic].s = true; isl[++ic].a = t; isl[ic].s = false; }

double ivl_merge() { int i,lv=0; double s,t=0; qsort(isl+1,ic,sizeof(isl[0]),cmp1); for (i=1;i<=ic;i++) { if (isl[i].s) { if (++lv == 1) s = isl[i].a; } else { if (–lv == 0) t += isl[i].a - s; } } return t; }

inline bool isin(double x,double x1,double x2) { if (x1 < x2) return x1 <= x && x <= x2; else return x2 <= x && x <= x1; }

void cross_segment(double x,point a,point b) { if (b.x == a.x || !isin(x,a.x,b.x)) return; double y = (b.y - a.y) * (x - a.x) / (b.x - a.x); y += a.y; if (y < miny) miny = y; if (y > maxy) maxy = y; }

void scan() { const double dx = 1e-6; double x; double per,lper=0; int p=0; for (x=Left;x<=Right;x+=dx) { ////// per = (x - Left)/(Right - Left) * 100; if (per - lper >=1) { lper = per; fprintf(stderr,"%.0lf percent\n",per); } ////// while (p+1 <=M && A[p+1].left <= x) DL.insert(&A[++p]); ic = 0; for (delist :: item *it = DL.front;it;it = it ->c[1]) { shape *S; for (;it;) { S = it -> e; if (x <= S->right) break; delist :: item *itn = it -> c[1]; DL.remove(it); it = itn; } if (!it) break;

        //Cross circle
        for (int i=0;i<2;i++)
        {
            if (S->c[i].x-R < x && x < S->c[i].x+R)
            {
                double tx,ty;
                tx = ABS(x - S->c[i].x);
                ty = sqrt(R*R - tx*tx);
                insert_ivl(S->c[i].y - ty , S->c[i].y + ty);
            }
        }
        
        miny = INF; maxy = -INF;
        cross_segment(x,S->v[0],S->v[1]);
        cross_segment(x,S->v[2],S->v[3]);
        cross_segment(x,S->v[0],S->v[2]);
        cross_segment(x,S->v[1],S->v[3]);
        insert_ivl(miny,maxy);
    }
    double t = ivl_merge();
    Total += t * dx;
}

}

void solve() { count_point(); qsort(A+1,M,sizeof(A[0]),cmp); scan(); printf("%.12lf\n",Total); }

int main() { int c_start,c_end; c_start = clock(); init(); solve(); c_end = clock(); cerr «“Running Time : " « double(c_end - c_start) / CLOCKS_PER_SEC « endl; return 0; }

上次修改时间 2017-05-26

问题简述

问题建模

解法 竖线扫描

算法描述

实际测试

参考程序

相关日志

解法竖线扫描