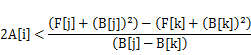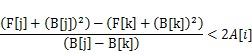NOI 2009 诗人小G

问题简述

有N个诗句需要被排版为若干行，顺序不能改变。一行内可以有若干个诗句，相邻诗句之间有一个空格。定义行标准长度L，每行的不协调度为|实际长度-L|^P，整首诗的不协调度就是每行不协调度之和。任务是安排一种排版方案，使得整首诗的不协调度最小。

问题建模

这是一个最优化问题，抽象成动态规划模型。设第i个诗句的长度为Len[i]，前i个诗句的总长度为SumL[i]，。F[i]为对前i个诗句排版的最小不协调度。

解法1 朴素的动态规划

算法描述

显然每个F[i]可以被分解为F[j]和第j+1…i个句子组成一行的状态，所以状态转移方程为

简化后，可以书写成

在具体实现时，应记录每个状态的决策，以便于输出合法方案。考虑到“最小的不协调度超过10¹⁸输出"Too hard to arrange"”，为防止64位整型运算溢出，可以先用浮点数类型计算，然后再用整型算出具体值。

复杂度分析

状态数为O(N)，每次转移需要以O(N)的时间枚举j，所以时间复杂度为O(N²)。在实际测试中通过了测试点1，2，3，得到30分。

参考程序

```cpp /* * Problem: NOI2009 poet * Author: Guo Jiabao * Time: 2009.9.22 13:30 * State: Solved * Memo: 朴素动态规划 */ #include #include #include #include #include using namespace std;

typedef long long big;

const int MAXN=100001,SMAXL=32; const big INF=~0ULL»1,LIMIT=1000000000000000000LL;

big F[MAXN],sumL[MAXN]; int N,L,P; int Len[MAXN],deci[MAXN],sel[MAXN]; char sent[MAXN][SMAXL];

void init() { scanf("%d%d%d\n",&N,&L,&P); for (int i=1;i<=N;++i) { gets(sent[i]); Len[i] = strlen(sent[i]); sumL[i] = sumL[i-1] + Len[i]; } }

big power(big a) { big t=1; double dt=1; if (a < 0) a = -a; for (int i=1;i<=P;i++) { dt *= a; if (dt > LIMIT) return INF; t *= a; } return t; }

void solve() { int i,j,k; big minv,t; for (i=1;i<=N;++i) { minv = INF; for (j=0;j<=i-1;++j) { t = power(sumL[i] - sumL[j] + i-j-1 - L); if ( double(t) + double(F[j]) <= LIMIT && t + F[j] < minv) { minv = t + F[j]; k = j; } } F[i] = minv; deci[i] = k; } }

void print() { if (F[N] <= LIMIT) { cout « F[N] « endl; int i,j; for (i=N,j=0;i;i=deci[i]) sel[++j] = i; for (i=0;j;j–) { for (++i;i < sel[j];++i) printf("%s “,sent[i]); printf("%s\n”,sent[i]); } } else printf(“Too hard to arrange\n”); printf("——————–\n"); }

int main() { int i,T; freopen(“poet.in”,“r”,stdin); freopen(“poet.out”,“w”,stdout); scanf("%d",&T); for (i=1;i<=T;i++) { init(); solve(); print(); } return 0; }


<h4>解法2 贪心的动态规划</h4>

<h5>算法描述</h5>
观察测试点4，5的N值较大，而L值较小，因此可以限制每行长度，以优化状态转移。

<a href="https://byvoid.com/attachments/wp/2010/01/clip_image008_thumb.gif"><img title="clip_image008" src="https://byvoid.com/attachments/wp/2010/01/clip_image008_thumb.gif" alt="clip_image008" width="455" height="55" /></a>

实现时应让j从i-1到0枚举，当j&lt;i-1时一旦发现行长度超过2L，即停止枚举j，因为j继续减少会让行长度继续增加。
<h5>算法证明</h5>
一个空行的不协调度为L<sup>P</sup>，若一行内包含多余一个句子，且行长度L’&gt;2L，则行不协调度(L’-L)<sup>P</sup>&gt;L<sup>P</sup>。把该行拆分为两行后，设长度分别为L1和L2，L1+L2=L’-1，拆分后的两行不协调度之和为(L1-L)P+(L2-L)P&lt;(L’-L)<sup>P</sup>，所以拆分为两行后比合在一行好。因此应保证当一行包含多于一个句子时，行长度&lt;=2L。
<h5>复杂度分析</h5>
状态数为O(N)，每次转移需要O(Min{N,L})的时间，所以时间复杂度为O(Min{N<sup>2</sup>,NL})。在实际测试中通过了前5个测试点，得到50分。
<h5>参考程序</h5>
```cpp
/* 
 * Problem: NOI2009 poet
 * Author: Guo Jiabao
 * Time: 2009.9.22 13:51
 * State: Solved
 * Memo: 朴素动态规划 剪枝
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
using namespace std;

typedef long long big;

const int MAXN=100001,SMAXL=32;
const big INF=~0ULL>>1,LIMIT=1000000000000000000LL;

big F[MAXN],sumL[MAXN];
int N,L,P;
int Len[MAXN],deci[MAXN],sel[MAXN];
char sent[MAXN][SMAXL];

void init()
{
	scanf("%d%d%d\n",&N,&L,&P);
	for (int i=1;i<=N;++i)
	{
		gets(sent[i]);
		Len[i] = strlen(sent[i]);
		sumL[i] = sumL[i-1] + Len[i];
	}
}

big power(big a)
{
	big t=1;
	double dt=1;
	if (a < 0)
		a = -a;
	for (int i=1;i<=P;i++)
	{
		dt *= a;
		if (dt > LIMIT)
			return INF;
		t *= a;
	}
	return t;
}

void solve()
{
	int i,j,k;
	big minv,t;
	for (i=1;i<=N;++i)
	{
		minv = INF;
		for (j=i-1;j>=0;--j)
		{
			t = sumL[i] - sumL[j] + i-j-1 - L;
			if (j < i-1 && t > L + L)
				break;
			t = power(t);
			if ( double(t) + double(F[j]) <= LIMIT && t + F[j] < minv)
			{
				minv = t + F[j];
				k = j;
			}
		}
		F[i] = minv;
		deci[i] = k;
	}
}

void print()
{
	if (F[N] <= LIMIT)
	{
		cout << F[N] << endl;
		int i,j;
		for (i=N,j=0;i;i=deci[i])
			sel[++j] = i;
		for (i=0;j;j--)
		{
			for (++i;i < sel[j];++i)
				printf("%s ",sent[i]);
			printf("%s\n",sent[i]);
		}
	}
	else
		printf("Too hard to arrange\n");
	printf("--------------------\n");
}

int main()
{
	int i,T;
	freopen("poet.in","r",stdin);
	freopen("poet.out","w",stdout);
	scanf("%d",&T);
	for (i=1;i<=T;i++)
	{
		init();
		solve();
		print();
	}
	return 0;
}

解法3 凸壳优化动态规划

算法描述

观察发现测试点6，7的N和L都很大，而P值为2。经分析发现可以使用单调队列维护凸壳。

算法分析与证明

当P=2时，观察状态转移方程

设对于F[i]的最优决策为k，那么对于所有的j≠k，均满足

设，，则有

因为SumL为单调增函数，所以A，B均为增函数。当B[j]>B[k] ⇒j>k，有

相对的，当j<k时有

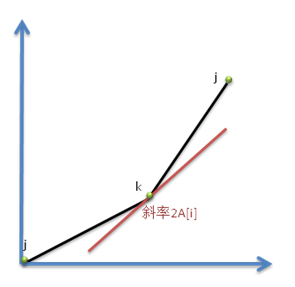
如果把(B[i],F[i]+B[i]²)看作是二维平面上的一个点，那么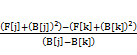恰为斜率公式。因此对于最优决策k，应保证在对应点右边任意一个决策j的对应点，满足直线kj斜率大于2A[i]；在对应点左边任意一个决策j的对应点，满足直线kj斜率小于2A[i]。

因此所有最优决策在平面上的对应点连线就是一个斜率递增的凸壳。

具体实现时，用单调队列维护每个点(B[i],F[i]+B[i]²)，每在队尾加入一个新的点，判断斜率是否递增，如果不是则不断删除队尾元素。求F[i]的最优决策只需不断在队首删除点，直到队首两点组成的直线斜率刚好大于2A[i]，最优决策就是左端点的对应决策。

复杂度分析

用单调队列每次维护凸壳的时间复杂度为均摊O(1)，所以时间复杂度为O(N)。经测试可以通过测试点6，7，配合解法2，一共可以得到70分。

参考程序

```cpp /* * Problem: NOI2009 poet * Author: Guo Jiabao * Time: 2009.9.22 14:30 * State: Solved * Memo: 朴素动态规划剪枝凸壳优化 */ #include #include #include #include #include using namespace std;

typedef long long big;

const int MAXN=100001,SMAXL=32; const big INF=~0ULL»1,LIMIT=1000000000000000000LL;

struct MonoQueue { struct point { big x,y; int id; }P[MAXN];

int head,tail;

void initialize()
{
	head = 0;
	tail = -1;
}

void insert(big x,big y,int id)
{
	point p={x,y,id};
	for (;head + 1 <= tail;--tail)
	{
		double k1,k2;
		k1 = (p.y - P[tail].y) / double(p.x - P[tail].x);
		k2 = (P[tail].y - P[tail-1].y) / double(P[tail].x - P[tail-1].x);
		if (k1 > k2)
			break;
	}
	P[++tail] = p;
}

int getmin(big v)
{
	for (;head + 1 <= tail;++head)
	{
		double k = (P[head+1].y - P[head].y) / double(P[head+1].x - P[head].x);
		if (k > v)
			break;
	}
	return P[head].id;
}

}MQ;

big F[MAXN],sumL[MAXN],A[MAXN],B[MAXN]; int N,L,P; int Len[MAXN],deci[MAXN],sel[MAXN]; char sent[MAXN][SMAXL];

void init() { scanf("%d%d%d\n",&N,&L,&P); for (int i=1;i<=N;++i) { gets(sent[i]); Len[i] = strlen(sent[i]); sumL[i] = sumL[i-1] + Len[i]; } }

big power(big a) { big t=1; double dt=1; if (a < 0) a = -a; for (int i=1;i<=P;i++) { dt *= a; if (dt > LIMIT) return INF; t *= a; } return t; }

void tq() { int i,j; big t; MQ.initialize(); MQ.insert(0,0,0); for (i=1;i<=N;i++) { B[i] = sumL[i] + i; A[i] = B[i] - 1 - L; } for (i=1;i<=N;i++) { j = MQ.getmin(A[i] + A[i]); t = power(sumL[i] - sumL[j] + i-j-1 - L); if ( double(t) + double(F[j]) <= LIMIT ) F[i] = F[j] + t; else F[i] = INF; if ( double(B[i]) * double(B[i]) + F[i] <= LIMIT) t = F[i] + B[i] * B[i]; else t = INF; MQ.insert(B[i],t,i); deci[i] = j; } }

void simple() { int i,j,k; big minv,t; k = -1; for (i=1;i<=N;++i) { minv = INF; for (j=i-1;j>=0;–j) { t = sumL[i] - sumL[j] + i-j-1 - L; if (t > L + L) break; t = power(t); if ( double(t) + double(F[j]) <= LIMIT && t + F[j] < minv) { minv = F[j] + t; k = j; } } F[i] = minv; deci[i] = k; } }

void solve() { if (P == 2) tq(); else simple(); }

int main() { int i,T; freopen(“poet.in”,“r”,stdin); freopen(“poet.out”,“w”,stdout); scanf("%d",&T); for (i=1;i<=T;i++) { init(); solve(); print(); } return 0; }


<h4>解法4 决策单调性优化动态规划</h4>

<h5>算法描述</h5>
可以观察到或证明出，该状态转移方程满足决策单调性。因此我们可以使用双端队列维护每个决策区间，对于每个新决策使用二分查找确定位置并更新决策队列。
<h5>算法证明</h5>
再次观察状态转移方程

<a href="https://byvoid.com/attachments/wp/2010/01/clip_image034_thumb.gif"><img title="clip_image034" src="https://byvoid.com/attachments/wp/2010/01/clip_image034_thumb.gif" alt="clip_image034" width="371" height="37" /></a><strong> </strong>

设<a href="https://byvoid.com/attachments/wp/2010/01/clip_image036_thumb.gif"><img title="clip_image036" src="https://byvoid.com/attachments/wp/2010/01/clip_image036_thumb.gif" alt="clip_image036" width="282" height="37" /></a>，状态转移方程可以化为1D/1D标准形式

<a href="https://byvoid.com/attachments/wp/2010/01/clip_image038_thumb.gif"><img title="clip_image038" src="https://byvoid.com/attachments/wp/2010/01/clip_image038_thumb.gif" alt="clip_image038" width="164" height="37" /></a>

要证明上述状态转移方程具有决策单调性，k(i)表示F[i]的最优决策，即

<a href="https://byvoid.com/attachments/wp/2010/01/clip_image040_thumb.gif"><img title="clip_image040" src="https://byvoid.com/attachments/wp/2010/01/clip_image040_thumb.gif" alt="clip_image040" width="104" height="37" /></a>

当且仅当满足四边形不等式

<a href="https://byvoid.com/attachments/wp/2010/01/clip_image042_thumb.gif"><img title="clip_image042" src="https://byvoid.com/attachments/wp/2010/01/clip_image042_thumb.gif" alt="clip_image042" width="359" height="37" /></a>

设<a href="https://byvoid.com/attachments/wp/2010/01/clip_image044_thumb.gif"><img title="clip_image044" src="https://byvoid.com/attachments/wp/2010/01/clip_image044_thumb.gif" alt="clip_image044" width="107" height="37" /></a>，<a href="https://byvoid.com/attachments/wp/2010/01/clip_image046_thumb.gif"><img title="clip_image046" src="https://byvoid.com/attachments/wp/2010/01/clip_image046_thumb.gif" alt="clip_image046" width="101" height="37" /></a>，<a href="https://byvoid.com/attachments/wp/2010/01/clip_image048_thumb.gif"><img title="clip_image048" src="https://byvoid.com/attachments/wp/2010/01/clip_image048_thumb.gif" alt="clip_image048" width="58" height="37" /></a>。其中<a href="https://byvoid.com/attachments/wp/2010/01/clip_image050_thumb.gif"><img title="clip_image050" src="https://byvoid.com/attachments/wp/2010/01/clip_image050_thumb.gif" alt="clip_image050" width="148" height="37" /></a>。

于是<a href="https://byvoid.com/attachments/wp/2010/01/clip_image052_thumb.gif"><img title="clip_image052" src="https://byvoid.com/attachments/wp/2010/01/clip_image052_thumb.gif" alt="clip_image052" width="152" height="37" /></a>。要证明①，只需证明

<a href="https://byvoid.com/attachments/wp/2010/01/clip_image054_thumb.gif"><img title="clip_image054" src="https://byvoid.com/attachments/wp/2010/01/clip_image054_thumb.gif" alt="clip_image054" width="570" height="37" /></a>

设<a href="https://byvoid.com/attachments/wp/2010/01/clip_image056_thumb.gif"><img title="clip_image056" src="https://byvoid.com/attachments/wp/2010/01/clip_image056_thumb.gif" alt="clip_image056" width="107" height="37" /></a>，<a href="https://byvoid.com/attachments/wp/2010/01/clip_image058_thumb.gif"><img title="clip_image058" src="https://byvoid.com/attachments/wp/2010/01/clip_image058_thumb.gif" alt="clip_image058" width="133" height="37" /></a>，则②等价于

<a href="https://byvoid.com/attachments/wp/2010/01/clip_image060_thumb.gif"><img title="clip_image060" src="https://byvoid.com/attachments/wp/2010/01/clip_image060_thumb.gif" alt="clip_image060" width="273" height="37" /></a>

<a href="https://byvoid.com/attachments/wp/2010/01/clip_image062_thumb.gif"><img title="clip_image062" src="https://byvoid.com/attachments/wp/2010/01/clip_image062_thumb.gif" alt="clip_image062" width="301" height="37" /></a>

因为<a href="https://byvoid.com/attachments/wp/2010/01/clip_image064_thumb.gif"><img title="clip_image064" src="https://byvoid.com/attachments/wp/2010/01/clip_image064_thumb.gif" alt="clip_image064" width="98" height="37" /></a>，且D[i+1]恒为正数，所以S&lt;T。于是要证明③，只需证明下列函数在整数域内(非严格)单调递增

<a href="https://byvoid.com/attachments/wp/2010/01/clip_image066_thumb.gif"><img title="clip_image066" src="https://byvoid.com/attachments/wp/2010/01/clip_image066_thumb.gif" alt="clip_image066" width="249" height="37" /></a><strong></strong>
<h6>(1)若P为偶数</h6>
<a href="https://byvoid.com/attachments/wp/2010/01/clip_image068_thumb.gif"><img title="clip_image068" src="https://byvoid.com/attachments/wp/2010/01/clip_image068_thumb.gif" alt="clip_image068" width="120" height="37" /></a>，求导得<a href="https://byvoid.com/attachments/wp/2010/01/clip_image070_thumb.gif"><img title="clip_image070" src="https://byvoid.com/attachments/wp/2010/01/clip_image070_thumb.gif" alt="clip_image070" width="169" height="37" /></a>。

因为<a href="https://byvoid.com/attachments/wp/2010/01/clip_image072_thumb.gif"><img title="clip_image072" src="https://byvoid.com/attachments/wp/2010/01/clip_image072_thumb.gif" alt="clip_image072" width="56" height="37" /></a>，P-1为奇数，所以<a href="https://byvoid.com/attachments/wp/2010/01/clip_image074_thumb.gif"><img title="clip_image074" src="https://byvoid.com/attachments/wp/2010/01/clip_image074_thumb.gif" alt="clip_image074" width="131" height="37" /></a>，<a href="https://byvoid.com/attachments/wp/2010/01/clip_image076_thumb.gif"><img title="clip_image076" src="https://byvoid.com/attachments/wp/2010/01/clip_image076_thumb.gif" alt="clip_image076" width="54" height="37" /></a>恒成立，f(x)在实数域内单调递增。
<h6>(2)若P为奇数</h6>
<h6>(a)当X-C&gt;=0</h6>
<a href="https://byvoid.com/attachments/wp/2010/01/clip_image0681_thumb.gif"><img title="clip_image068[1]" src="https://byvoid.com/attachments/wp/2010/01/clip_image0681_thumb.gif" alt="clip_image068[1]" width="120" height="37" /></a>，求导得<a href="https://byvoid.com/attachments/wp/2010/01/clip_image0701_thumb.gif"><img title="clip_image070[1]" src="https://byvoid.com/attachments/wp/2010/01/clip_image0701_thumb.gif" alt="clip_image070[1]" width="169" height="37" /></a>。

因为<a href="https://byvoid.com/attachments/wp/2010/01/clip_image080_thumb.gif"><img title="clip_image080" src="https://byvoid.com/attachments/wp/2010/01/clip_image080_thumb.gif" alt="clip_image080" width="82" height="37" /></a>，P-1为偶数，所以<a href="https://byvoid.com/attachments/wp/2010/01/clip_image0741_thumb.gif"><img title="clip_image074[1]" src="https://byvoid.com/attachments/wp/2010/01/clip_image0741_thumb.gif" alt="clip_image074[1]" width="131" height="37" /></a>，<a href="https://byvoid.com/attachments/wp/2010/01/clip_image0761_thumb.gif"><img title="clip_image076[1]" src="https://byvoid.com/attachments/wp/2010/01/clip_image0761_thumb.gif" alt="clip_image076[1]" width="54" height="37" /></a>恒成立，f(x)在实数域内单调递增。
<h6>(b)当X&lt;=0</h6>
<a href="https://byvoid.com/attachments/wp/2010/01/clip_image084_thumb.gif"><img title="clip_image084" src="https://byvoid.com/attachments/wp/2010/01/clip_image084_thumb.gif" alt="clip_image084" width="142" height="37" /></a>，求导得<a href="https://byvoid.com/attachments/wp/2010/01/clip_image086_thumb.gif"><img title="clip_image086" src="https://byvoid.com/attachments/wp/2010/01/clip_image086_thumb.gif" alt="clip_image086" width="172" height="37" /></a>。因为P-1为偶数，<a href="https://byvoid.com/attachments/wp/2010/01/clip_image0762_thumb.gif"><img title="clip_image076[2]" src="https://byvoid.com/attachments/wp/2010/01/clip_image0762_thumb.gif" alt="clip_image076[2]" width="54" height="37" /></a>恒成立，f(x)在实数域内单调递增。
<h6>(c)当0&lt;X&lt;C</h6>
<a href="https://byvoid.com/attachments/wp/2010/01/clip_image090_thumb.gif"><img title="clip_image090" src="https://byvoid.com/attachments/wp/2010/01/clip_image090_thumb.gif" alt="clip_image090" width="120" height="37" /></a>，求导得<a href="https://byvoid.com/attachments/wp/2010/01/clip_image0861_thumb.gif"><img title="clip_image086[1]" src="https://byvoid.com/attachments/wp/2010/01/clip_image0861_thumb.gif" alt="clip_image086[1]" width="172" height="37" /></a>。因为P-1为偶数，<a href="https://byvoid.com/attachments/wp/2010/01/clip_image0763_thumb.gif"><img title="clip_image076[3]" src="https://byvoid.com/attachments/wp/2010/01/clip_image0763_thumb.gif" alt="clip_image076[3]" width="54" height="37" /></a>恒成立，f(x)在实数域内单调递增。

综上所述，f(x)在实数域内单调递增，即在正数域内单调递增，因而③②①依次得证。

因此状态转移方程<a href="https://byvoid.com/attachments/wp/2010/01/clip_image0061_thumb.gif"><img title="clip_image006[1]" src="https://byvoid.com/attachments/wp/2010/01/clip_image0061_thumb.gif" alt="clip_image006[1]" width="357" height="37" /></a>具有决策单调性。
<h5>复杂度分析</h5>
状态数为O(N)，每次维护决策队列的时间为O(logN)，所以时间复杂度为O(NlogN)。在测试中通过了全部测试点，拿到了100分。
<h5>参考程序</h5>
```cpp
/* 
 * Problem: NOI2009 poet
 * Author: Guo Jiabao
 * Time: 2009.9.22 16:30
 * State: Solved
 * Memo: 动态规划 决策单调性
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
using namespace std;

typedef long long big;

const int MAXN=100001,SMAXL=32;
const big LIMIT=1000000000000000000LL;

struct interval
{
	int s,t,deci;
}di[MAXN];

double F[MAXN];
int N,L,P,Stop;
int Len[MAXN],deci[MAXN],sel[MAXN];
char sent[MAXN][SMAXL];
big G[MAXN],sumL[MAXN];

void init()
{
	scanf("%d%d%d\n",&N,&L,&P);
	for (int i=1;i<=N;++i)
	{
		gets(sent[i]);
		Len[i] = strlen(sent[i]);
		sumL[i] = sumL[i-1] + Len[i];
	}
}

double dpower(double a)
{
	double t=1;
	if (a < 0)
		a = -a;
	for (int i=1;i<=P;i++)
		t *= a;
	return t;
}

double getF(int i,int j)
{
	double t = dpower(sumL[i] - sumL[j] + i-j-1 - L);
	return F[j] + t;
}

big power(big a)
{
	big t=1;
	double dt=1;
	if (a < 0)
		a = -a;
	for (int i=1;i<=P;i++)
	{
		dt *= a;
		if (dt > LIMIT)
			return LIMIT+1;
		t *= a;
	}
	return t;
}

big getG(int i,int j)
{
	big t = power(sumL[i] - sumL[j] + i-j-1 - L);
	if (F[j] + t <= LIMIT)
		return G[j] + t;
	else
		return LIMIT + 1;
}

void update(int i)
{
	while (di[Stop].s > i && getF(di[Stop].s,i) < getF(di[Stop].s,di[Stop].deci) )
	{
		di[Stop-1].t = di[Stop].t;
		Stop --;
	}
	int a=di[Stop].s,b=di[Stop].t,m;
	if (a < i+1)
		a = i+1;
	while (a+1<b)
	{
		m = (a + b) >> 1;
		if ( getF(m,di[Stop].deci) < getF(m,i) )
			a = m;
		else
			b = m-1;
	}
	if ( a < b && getF(b,di[Stop].deci) < getF(b,i) )
		a = b;
	if (a+1 <= di[Stop].t)
	{
		di[Stop + 1].s = a+1;
		di[Stop + 1].t = di[Stop].t;
		di[Stop + 1].deci = i;
		di[Stop].t = a;
		++Stop;
	}
}

void solve()
{
	int i,j;
	di[Stop=1].s = 1;
	di[Stop].t = N;
	for (i=j=1;i<=N;i++)
	{
		if (i > di[j].t)
			++j;
		deci[i] = di[j].deci;
		F[i] = getF(i,deci[i]);
		update(i);
	}
	for (i=1;i<=N;i++)
		G[i] = getG(i,deci[i]);
}

void print()
{
	if (G[N] <= LIMIT)
	{
		cout << G[N] << endl;
		int i,j;
		for (i=N,j=0;i;i=deci[i])
			sel[++j] = i;
		for (i=0;j;j--)
		{
			for (++i;i < sel[j];++i)
				printf("%s ",sent[i]);
			printf("%s\n",sent[i]);
		}
	}
	else
		printf("Too hard to arrange\n");
	printf("--------------------\n");
}

int main()
{
	int i,T;
	freopen("poet.in","r",stdin);
	freopen("poet.out","w",stdout);
	scanf("%d",&T);
	for (i=1;i<=T;i++)
	{
		init();
		solve();
		print();
	}
	return 0;
}

上次修改时间 2017-05-26

问题简述

问题建模

解法1 朴素的动态规划

算法描述

复杂度分析

参考程序

解法3 凸壳优化动态规划

算法描述

算法分析与证明

复杂度分析

参考程序

相关日志