本文正體字版由OpenCC轉換
這道題正確的解法是構造網絡,求網絡最小費用最大流,但是模型隱藏得較深,不易想到。構造網絡是該題的關鍵,以下面一個例子說明構圖的方法和解釋。
例如一共需要4天,四天需要的人數依次是4,2,5,3。有5類志願者,如下表所示:
| 種類 | 1 | 2 | 3 | 4 | 5 |
| 時間 | 1-2 | 1-1 | 2-3 | 3-3 | 3-4 |
| 費用 | 3 | 4 | 3 | 5 | 6 |
設僱傭第i類志願者的人數爲X[i],每個志願者的費用爲V[i],第j天僱傭的人數爲P[j],則每天的僱傭人數應滿足一個不等式,如上表所述,可以列出
P[1] = X[1] + X[2] >= 4
P[2] = X[1] + X[3] >= 2
P[3] = X[3] + X[4] +X[5] >= 5
P[4] = X[5] >= 3
對於第i個不等式,添加輔助變量Y[i] (Y[i]>=0) ,可以使其變爲等式
P[1] = X[1] + X[2] - Y[1] = 4
P[2] = X[1] + X[3] - Y[2] = 2
P[3] = X[3] + X[4] +X[5] - Y[3] = 5
P[4] = X[5] - Y[4] = 3
在上述四個等式上下添加P[0]=0,P[5]=0,每次用下邊的式子減去上邊的式子,得出
① P[1] - P[0] = X[1] + X[2] - Y[1] = 4
② P[2] - P[1] = X[3] - X[2] -Y[2] +Y[1] = -2
③ P[3] - P[2] = X[4] + X[5] - X[1] - Y[3] + Y[2] =3
④ P[4] - P[3] = - X[3] - X[4] + Y[3] - Y[4] = -2
⑤ P[5] - P[4] = - X[5] + Y[4] = -3
觀察發現,每個變量都在兩個式子中出現了,而且一次爲正,一次爲負。所有等式右邊和爲0。接下來,根據上面五個等式構圖。
-
每個等式爲圖中一個頂點,添加源點S和匯點T。
-
如果一個等式右邊爲非負整數c,從源點S向該等式對應的頂點連接一條容量爲c,權值爲0的有向邊;如果一個等式右邊爲負整數c,從該等式對應的頂點向匯點T連接一條容量爲c,權值爲0的有向邊。
-
如果一個變量X[i]在第j個等式中出現爲X[i],在第k個等式中出現爲-X[i],從頂點j向頂點k連接一條容量爲∞,權值爲V[i]的有向邊。
-
如果一個變量Y[i]在第j個等式中出現爲Y[i],在第k個等式中出現爲-Y[i],從頂點j向頂點k連接一條容量爲∞,權值爲0的有向邊。
構圖以後,求從源點S到匯點T的最小費用最大流,費用值就是結果。
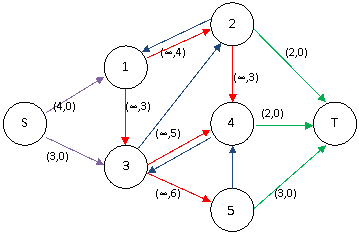
根據上面的例子可以構造出如下網絡,紅色的邊爲每個變量X代表的邊,藍色的邊爲每個變量Y代表的邊,邊的容量和權值標已經標出(藍色沒有標記,因爲都是容量∞,權值0)。
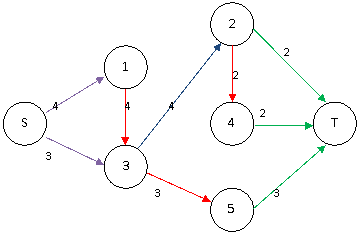
在這個圖中求最小費用最大流,流量網絡如下圖,每個紅色邊的流量就是對應的變量X的值。
所以,答案爲43+23+3*6=36。
上面的方法很神奇得求出了結果,思考爲什麼這樣構圖。我們將最後的五個等式進一步變形,得出以下結果
① - X[1] - X[2] + Y[1] + 4 = 0
② - X[3] + X[2] + Y[2] - Y[1] - 2 = 0
③ - X[4] - X[5] + X[1] + Y[3] - Y[2] + 3 = 0
④ X[3] + X[4] - Y[3] + Y[4] - 2 = 0
⑤ X[5] - Y[4] - 3 = 0
可以發現,每個等式左邊都是幾個變量和一個常數相加減,右邊都爲0,恰好就像網絡流中除了源點和匯點的頂點都滿足流量平衡。每個正的變量相當於流入該頂點的流量,負的變量相當於流出該頂點的流量,而正常數可以看作來自附加源點的流量,負的常數是流向附加匯點的流量。因此可以據此構造網絡,求出從附加源到附加匯的網絡最大流,即可滿足所有等式。而我們還要求![]() 最小,所以要在X變量相對應的邊上加上權值,然後求最小費用最大流。
最小,所以要在X變量相對應的邊上加上權值,然後求最小費用最大流。
我寫的是樸素的SPFA算法求增廣路的最小費用流算法,可以在題目時限內通過所有測試點。
在NOI的現場上,該題得分的平均分12.56,只有高逸涵大牛拿到了滿分。不能不說這是一道難題,難就難在抽象出問題的數學模型,設計有效的算法。而信息學競賽正朝着這個方向發展,數學建模將是解決問題的共同關鍵步驟。
/*
* Problem: NOI2008 employee
* Author: Guo Jiabao
* Time: 2009.3.2 14:03
* State: Solved
* Memo: SPFA最小費用最大流
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
const int MAXN=1003,MAXM=10002*4,INF=0x7FFFFFFF;
using namespace std;
struct edge
{
edge *next,*op;
int t,c,v;
}ES[MAXM],*V[MAXN];
struct Queue
{
int Q[MAXN],QH,QL,Size;
bool inq[MAXN];
inline void ins(int v)
{
if (++QL>=MAXN)
QL=0;
Q[QL]=v;
inq[v]=true;
Size++;
}
inline int pop()
{
int r=Q[QH];
inq[r]=false;
Size--;
if (++QH>=MAXN)
QH=0;
return r;
}
inline void reset()
{
memset(Q,0,sizeof(Q));
QH=Size=0;
QL=-1;
}
}Q;
int N,M,S,T,EC=-1;
int demond[MAXN],sp[MAXN],prev[MAXN];
edge *path[MAXN];
inline void addedge(int a,int b,int v,int c=INF)
{
edge e1={V[a],0,b,c,v} , e2={V[b],0,a,0,-v};
ES[++EC]=e1; V[a]=&ES[EC];
ES[++EC]=e2; V[b]=&ES[EC];
V[a]->op=V[b]; V[b]->op=V[a];
}
void init()
{
int i,a,b,c;
freopen("employee.in","r",stdin);
freopen("employee.out","w",stdout);
scanf("%d%d",&N,&M);
for (i=1;i<=N;i++)
scanf("%d",&demond[i]);
for (i=1;i<=M;i++)
{
scanf("%d%d%d",&a,&b,&c);
addedge(a,b+1,c);
}
S=0,T=N+2;
for (i=1;i<=N+1;i++)
{
c = demond[i] - demond[i-1];
if (c>=0)
addedge(S,i,0,c);
else
addedge(i,T,0,-c);
if (i>1)
addedge(i,i-1,0);
}
}
bool spfa()
{
int u,v;
for (u=S;u<=T;u++)
sp[u]=INF;
Q.reset();
Q.ins(S);
sp[S]=0;
prev[S]=-1;
while (Q.Size)
{
u=Q.pop();
for (edge *k=V[u];k;k=k->next)
{
v=k->t;
if (k->c>0 && sp[u] + k->v <sp[v])
{
sp[v]=sp[u] + k->v;
prev[v]=u;
path[v]=k;
if (!Q.inq[v])
Q.ins(v);
}
}
}
return sp[T]!=INF;
}
int argument()
{
int i,delta=INF,flow=0;
edge *e;
for (i=T;prev[i]!=-1;i=prev[i])
{
e=path[i];
if (e->c<delta)
delta=e->c;
}
for (i=T;prev[i]!=-1;i=prev[i])
{
e=path[i];
e->c-=delta;e->op->c+=delta;
flow+=e->v*delta;
}
return flow;
}
int maxcostflow()
{
int Flow=0;
while (spfa())
Flow += argument();
return Flow;
}
int main()
{
init();
printf("%dn",maxcostflow());
return 0;
}
<h2><span class="mw-headline">志願者招募 </span></h2>
【問題描述】
申奧成功後,布布經過不懈努力,終於成爲奧組委下屬公司人力資源部門的主管。布布剛上任就遇到了一個難題:爲即將啓動的奧運新項目招募一批短期志願者。經過估算,這個項目需要N 天才能完成,其中第i 天至少需要Ai 個人。
布布通過了解得知,一共有M 類志願者可以招募。其中第i 類可以從第Si 天工作到第Ti 天,招募費用是每人Ci 元。新官上任三把火,爲了出色地完成自己的工作,布布希望用盡量少的費用招募足夠的志願者,但這並不是他的特長!於是布布找到了你,希望你幫他設計一種最 優的招募方案。
【輸入格式】
輸入文件的第一行包含兩個整數N, M,表示完成項目的天數和可以招募的志願者的種類。
接下來的一行中包含N 個非負整數,表示每天至少需要的志願者人數。
接下來的M 行中每行包含三個整數Si, Ti, Ci,含義如上文所述。爲了方便起見,我們可以認爲每類志願者的數量都是無限多的。
【輸出格式】
輸入文件中僅包含一個整數,表示你所設計的最優方案的總費用。
【輸入樣例】
<pre>3 3
2 3 4
1 2 2
2 3 5
3 3 2</pre>
【輸出樣例】
<pre>14</pre>
【樣例說明】
-
招募3 名第一類志願者和4 名第三類志願者。
【數據規模和約定】
-
30%的數據中,1 ≤ N, M ≤ 10,1 ≤ Ai ≤ 10;
-
100%的數據中,1 ≤ N ≤ 1000,1 ≤ M ≤ 10000,題目中其他所涉及的數據均
不超過2^31-1。
上次修改時間 2017-05-26