本文正體字版由OpenCC轉換
問題簡述
有一些植物,每個植物攜帶有一定的資源(可正可負),且有一個攻擊範圍,可以保護攻擊位置上的另一個植物。有一羣殭屍從右向左進攻植物,殭屍不能走到植物的攻擊範圍內。任務是求一個進攻方案,使得殭屍獲得的資源儘可能多。
問題建模
首先我們我建立圖論模型,把每個植物當做一個頂點,植物攜帶的資源數目爲頂點的權值。如果一個植物b在另一個植物a的攻擊範圍內,連接一條有向邊<a,b>,表示a可以保護b。由於殭屍從右向左進攻,可以認爲每個植物都被它右邊相鄰的植物保護,對於每個植物a(除最左邊一列),向其左邊的相鄰植物b,連接一條有向邊<a,b>。
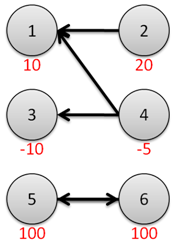
題目中給出的樣例建圖後如下所示
觀察上圖發現,{5,6}互相依賴,不可能被攻擊到。我們可以用拓撲排序去除圖中的環依賴結構,以簡化圖。
解法1 搜索
算法描述
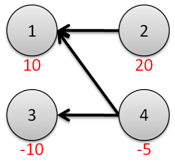
建模後,直接觀察發現可以搜索。每次尋找一個入度爲0的頂點,嘗試攻擊它,更新它指向的點的入度繼續搜索。搜索中記錄選取的頂點的權值之和,保留最大值。複雜度分析
搜索的時間複雜度爲O(MN)。在實際測試中得到40分。參考程序
```cpp /* * Problem: NOI2009 pvz * Author: Guo Jiabao * Time: 2009.7.29 12:01 * State: Solved * Memo: 暴力搜索 */ #includeusing namespace std;
const int MAXN=603,MAXM=MAXNMAXN4,INF=~0U»1;
struct edge { edge *next; int t; }*V[MAXN],ES[MAXM];
FILE *fi,*fo;
int R,C,EC,Ans,Maxflow,Stop,S,T,N; int score[MAXN],ind[MAXN]; bool vis[MAXN];
inline void addedge(int a,int b) { ES[++EC].next = V[a]; V[a] = ES+EC; V[a]->t = b; }
inline int point2id(int x,int y) { return x * C + y + 1; }
void init() { int i,j,k,l,q,x,y,s,c; fi = fopen(“pvz.in”,“r”); fo = fopen(“pvz.out”,“w”); fscanf(fi,"%d%d",&R,&C); for (i=0;i<R;i++) { for (j=0;j<C;j++) { k = point2id(i,j); if (j+1<C) { q = point2id(i,j+1); addedge(q,k); ind[k]++; } fscanf(fi,"%d%d",&s,&c); score[k] = s; for (l=1;l<=c;l++) { fscanf(fi,"%d%d",&x,&y); q = point2id(x,y); addedge(k,q); ind[q]++; } } } N=R*C; }
void dfs(int s) { if (s > Ans) Ans = s; int i; edge *e; for (i=1;i<=N;i++) if (ind[i] == 0 && !vis[i]) { vis[i]=true; for (e=V[i];e;e=e->next) ind[ e->t ]–; dfs(s+score[i]); vis[i]=false; for (e=V[i];e;e=e->next) ind[ e->t ]++; } }
void solve() { Ans = 0; dfs(0); fprintf(fo,"%d\n",Ans); fclose(fi); fclose(fo); }
int main() { init(); solve(); return 0; }
<h4><a name="_Toc241653483">解法</a>2 最大封閉子圖</h4>
<h5><a name="_Toc241653484">算法描述</a></h5>
將圖轉置後發現,一個合法的攻擊方案是一個<strong>封閉子圖</strong>(Closure of a Graph),我們的目標就是最大化攻擊方案的點權值和,就是要求一個<strong>最大封閉子圖</strong>(Maximum Weight Closure of a Graph),只需轉化爲網絡流模型,即可解決。
<h5><a name="_Toc241653485">算法分析</a></h5>
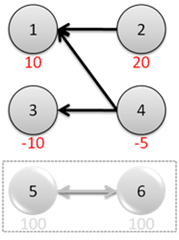
樣例的圖轉置後如下,其最大封閉子圖爲{1,2,4}。
<a href="https://byvoid.com/attachments/wp/2010/01/image8.png"><img title="image" src="https://byvoid.com/attachments/wp/2010/01/image8.png" alt="image" width="175" height="166" /></a>
最大封閉子圖的玩網絡流建模方法爲:
1. 建立附加源S和附加匯T。
2. 圖中原有的邊容量設爲∞。
3. 從S向每個權值爲正的點連接一條容量爲該點權值的有向邊。
4. 從每個權值不爲正的點向T連接一條容量爲該點權值絕對值的有向邊。
在網絡上求S到T的網絡最大流Maxflow,最大封閉子圖的權值就是(所有正權點權值之和 – Maxflow)。
樣例建模後如下圖所示,求得Maxflow = 5,所以最大封閉子圖的權值爲(10 + 20 – 5) = 25。
<a href="https://byvoid.com/attachments/wp/2010/01/image9.png"><img title="image" src="https://byvoid.com/attachments/wp/2010/01/image9.png" alt="image" width="175" height="404" /></a>
求最大封閉子圖的網絡流建模方法的嚴格證明見胡伯濤《最小割模型在信息學競賽中的應用》。
<h5><a name="_Toc241653486">複雜度分析</a></h5>
該圖點數爲O(NM),邊數可達O(N<sup>2</sup>M<sup>2</sup>)。拓撲排序和建圖的時間爲O(N<sup>2</sup>M<sup>2</sup>),用Dinic算法求網絡最大流的時間爲O(|V|<sup>2</sup>|E|),所以總時間複雜度爲O(N<sup>4</sup>M<sup>4</sup>)。在實際測試中通過了所以測試點,得到100分。
<h5><a name="_Toc241653487">參考程序</a></h5>
```cpp
/*
* Problem: NOI2009 pvz
* Author: Guo Jiabao
* Time: 2009.7.29 11:52
* State: Solved
* Memo: 最大封閉子圖 網絡最大流
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
using namespace std;
const int MAXN=603,MAXM=MAXN*MAXN*4,INF=~0U>>1;
struct edge
{
edge *next,*op;
int t,c;
}*V[MAXN],*V0[MAXN],*P[MAXN],ES[MAXM],*Stae[MAXN];
FILE *fi,*fo;
int R,C,EC,Ans,Maxflow,Stop,S,T,N;
int score[MAXN],ind[MAXN],Lv[MAXN],Stap[MAXN],Q[MAXN];
bool ts[MAXN];
inline void addedge(edge **V,int a,int b,int c)
{
ES[++EC].next = V[a]; V[a] = ES+EC; V[a]->t = b; V[a]->c=c;
ES[++EC].next = V[b]; V[b] = ES+EC; V[b]->t = a; V[b]->c=0;
V[a]->op = V[b]; V[b]->op = V[a];
}
inline int point2id(int x,int y)
{
return x * C + y + 1;
}
void init()
{
int i,j,k,l,q,x,y,s,c;
fi = fopen("pvz.in","r");
fo = fopen("pvz.out","w");
fscanf(fi,"%d%d",&R,&C);
for (i=0;i<R;i++)
{
for (j=0;j<C;j++)
{
k = point2id(i,j);
if (j+1<C)
{
q = point2id(i,j+1);
addedge(V0,q,k,1);
ind[k]++;
}
fscanf(fi,"%d%d",&s,&c);
score[k] = s;
for (l=1;l<=c;l++)
{
fscanf(fi,"%d%d",&x,&y);
q = point2id(x,y);
addedge(V0,k,q,1);
ind[q]++;
}
}
}
N=R*C;
}
void topsort()
{
int i,j;
Stop = 0;
for (i=1;i<=N;i++)
if (ind[i]==0)
Stap[++Stop] = i;
while (Stop)
{
i = Stap[Stop--];
ts[i] = true;
for (edge *e=V0[i];e;e=e->next)
{
j=e->t;
if (e->c)
{
ind[j]--;
if (ind[j] == 0)
Stap[++Stop] = j;
}
}
}
}
void makegraph()
{
int i,j;
S=0;
T=N+1;
for (i=1;i<=N;i++)
if (ts[i])
{
if (score[i] > 0)
{
addedge(V,S,i,score[i]);
Ans += score[i];
}
else
addedge(V,i,T,-score[i]);
for (edge *e=V0[i];e;e=e->next)
{
j=e->t;
if (ts[j] && e->c)
{
addedge(V,j,i,INF);
}
}
}
}
bool Dinic_label()
{
int i,j,head,tail;
memset(Lv,0,sizeof(Lv));
Q[head=tail=0] = S;
Lv[S] = 1;
while (head<=tail)
{
i = Q[head++];
for (edge *e=V[i];e;e=e->next)
{
j = e->t;
if (Lv[j] == 0 && e->c)
{
Lv[j] = Lv[i]+1;
if (j==T)
return true;
Q[++tail] = j;
}
}
}
return false;
}
void Dinic_aug()
{
int i,j,delta;
for (i=S;i<=T;i++)
P[i] = V[i];
Stap[Stop=1]=S;
while (Stop)
{
i = Stap[Stop];
if (i!=T)
{
for (;P[i];P[i]=P[i]->next)
if (P[i]->c && Lv[ j = P[i]->t ] == Lv[i] + 1)
break;
if (P[i])
{
Stap[++Stop] = j;
Stae[Stop] = P[i];
}
else
Stop--,Lv[i] = 0;
}
else
{
delta = INF;
for (i=Stop;i>=2;i--)
if (Stae[i]->c < delta)
delta = Stae[i]->c;
for (i=Stop;i>=2;i--)
{
Stae[i]->c -= delta;
Stae[i]->op->c += delta;
if (Stae[i]->c == 0)
Stop = i-1;
}
Maxflow += delta;
}
}
}
void Dinic()
{
while (Dinic_label())
Dinic_aug();
}
void solve()
{
topsort();
makegraph();
Dinic();
Ans -= Maxflow;
fprintf(fo,"%d\n",Ans);
fclose(fi);
fclose(fo);
}
int main()
{
init();
solve();
return 0;
}
上次修改時間 2017-05-26