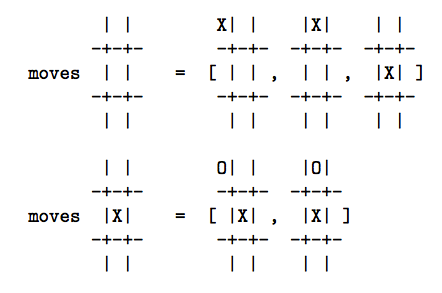函數式程序設計爲什麼至關重要

本文正體字版由OpenCC轉換

Why Functional Programming Matters 函數式程序設計爲什麼至關重要

作者： John Hughes 原文地址：http://wiht.link/functional-prog

此論文作於1984年，作爲查麥茲大學的備忘錄流傳了多年，經過小幅度修訂的版本出現於1989年與1990年，即［Hug89］與［Hug90］。此版本基於原查麥茲大學備忘錄的nroff源碼，爲LaTeX做了改動,使其更接近於印刷版本並糾正了少許錯誤。

本文由CloudiDust在 http://blog.csdn.net/ddwn/article/details/984390 最初翻譯，並由BYVoid根據原文重新校對、整理和排版。

摘要

軟件正在變得越來越複雜，因此良好的軟件構架也越來越重要。結構良好的軟件易於編寫，易於除錯，同時提供可複用組件庫以降低未來開發的成本。傳統型語言在程序模塊化方面具有理念上的侷限性，而函數式語言超越了局限。在本文中我們指出，函數式語言的兩大特性，高階函數與惰性求值，能夠極大地促進模塊化。作爲例證，我們處理了列表和樹，編寫了一些數值算法，並實現了alpha-beta啓發式搜索（一個人工智能算法，用於遊戲系統中）。既然模塊化是程序設計成功的關鍵，那麼函數式語言對現實世界而言便極其重要了。

1.引言

本論文試圖證明，對“現實世界”而言，函數式程序設計是極其重要的。同時，本文也試圖明確指出函數式語言的長處，以幫助使用函數式語言的程序員們將這些長處發揮到極致。

函數式語言之所以被如此稱呼，是因爲程序完全是由函數組成的。主程序本身也是一個函數，以程序的輸入爲參數，並返回其輸出。典型地，主函數通過其他函數定義，而這些函數又同樣以更多的其他函數來定義，直到最低層的語言原生函數爲止。這些函數與數學中的函數很相像，因此在本文中將以普通等式來定義它們。本文使用了Turner的程序語言Miranda中的表示方法，但對於之前沒有函數式語言相關知識的讀者，本文仍然是可讀的。（Miranda是Research Software Ltd.的商標。）

函數式程序設計的特性與優點通常總結爲類似這樣：函數式程序不包含任何賦值語句，因此變量一旦被賦予一個值，就不再改變。更一般地說，函數式程序不包含任何副作用：一個函數除了計算它本身的值以外，不產生任何作用。這一特性消滅了“Bug”的一個主要來源，同時也使執行順序不再重要——沒有副作用能夠改變一個表達式的值，故它可以在任何時刻被求值。這一特性將程序員從決定控制流的重擔之下拯救出來。由於表達式可以在任何時刻被求值，程序員便可以隨心所欲地使用變量的值來代替變量，反之亦然——也就是說，程序是“引用透明”的。這一自由使得函數式程序與它們傳統的對應物相比，更容易數學化地控制。

這樣的“優點”列表很不錯，但如果說外行人不把它當回事，這也並不會令人驚訝。它列出了很多內容關於函數式程序設計“沒有”什麼（它沒有賦值，沒有副作用，沒有控制流）但卻沒多說它“有”什麼。函數式程序員聽起來很像是中世紀的僧侶似的，他們禁絕了塵世中的種種樂趣並且期望這能使自己變得高潔。對於那些更關心物質利益的人而言，這些“優點”並沒有多大的說服力。

函數式程序員們爭辯說，函數式程序設計確實有巨大的物質利益——一個函數式程序員擁有比他傳統型的同行高得多的生產力，因爲函數式程序短得多。但這有什麼道理嗎？在這些“優點”的基礎之上，唯一的很靠不住的藉口就是，傳統的程序中有90％是賦值語句，而在函數式程序中這些全都可以省略！這真是太荒唐了，如果省略賦值語句可以帶來如此巨大的好處，那麼FORTRAN程序員們早該這樣幹了二十年了。通過省略特性來使語言更加強大在邏輯上是不可能的，不論這種特性是多麼糟糕。

甚至函數式程序員都應該對這些所謂的“優點”表示不滿意，因爲它們對於發掘函數式語言的威力毫無幫助。不可能寫出一個特別地（particularly）缺少了賦值語句或者特別地引用透明的程序。這些不是什麼衡量程序質量的尺度，因此盯緊了它們（以此證明函數式語言的強大）也不理想。

很明顯，對函數式程序設計的特性的描述是不完備的。我們必須找出一些東西來填補——它們不但要解釋函數式程序設計的威力，更要給函數式程序員們一個明確的追求目標。

2.與結構化程序設計的相似性

指出函數式與結構化程序設計之間的相似性是很有幫助的。過去，結構化程序設計的特性與優點被總結爲類似這樣：結構化程序不包含goto語句；結構化程序中的語句塊沒有多入口與多出口；結構化程序與它們傳統的對應物相比，更容易數學化地控制。這些結構化程序設計的“優點”與我們之前所談到的函數式程序設計的“優點”在本質上很相似。這些敘述本質上都是否定式的，從而導致了諸如“不可或缺的goto”之類一大堆徒勞的爭論。

事後諸葛亮式地說，很明顯地，結構化程序設計的這些特性，儘管很有用，但沒有觸及問題的核心。結構化程序與非結構化程序之間最重要的區別就是，結構化程序是用模塊化的方法設計的。模塊化設計帶來了生產力的巨大提升：首先，小模塊可以很快很容易地編寫；其次，通用模塊可以被重用，使以後的程序可以更快地開發；再次，程序的模塊可以被獨立測試，減少了除錯的時間。

“不使用goto”等等這一類特性，對於這一提升沒什麼作用。這些特性促進了“程序設計的小改良”，然而模塊化設計卻促進了“程序設計的大進化”。因此，程序員在FORTRAN或彙編語言中都可以享受結構化程序設計帶來的好處，哪怕那需要一點額外的工作。

模塊化設計是成功的程序設計的關鍵，這一觀點現在已經被普遍地接受了，而諸如Modula-II[Wir82]，Ada[oD80]以及Standard ML[MTH90]之類的程序語言都內置了語言特性以促進模塊化。然而，有一點非常重要，卻常常被忽略。當編寫一個模塊化程序以解決問題的時候，程序員首先把這個問題分解爲子問題，而後解決這些子問題並把解決方案合併。程序員能夠以什麼方式分解問題，直接取決於他能以什麼方式把解決方案粘起來。因此，爲了能在觀念上提升程序員將問題模塊化的能力，必須在程序語言提供中提供各種新的黏合劑。複雜的作用域規則與對分塊編譯的支持只對文本層面的細節有幫助，它們沒有提供能表達新觀念的工具以分解問題。

通過與木匠行業的類比可以認識到黏合劑的重要性。先製作椅子的各部分——坐墊，椅子腿，靠背，等等——而後用正確的方法釘起來，那麼製作一把椅子是很容易的。但這取決於將木板與插接口結合起來的能力。如果缺乏這種能力，那麼製作椅子的唯一方式，就是將它從一大塊木頭裏整個地切割出來，這是一項艱鉅得多的任務。這個例子同時表明了模塊化的非凡威力與擁有合適的黏合劑的重要性。

現在讓我們回到函數式程序設計上來。在這篇論文餘下的部分裏，我們將指出，函數式語言提供了兩種新的、非常重要的黏合劑。我們將給出許多可以使用新方法模塊化的示例程序，它們因此變得很簡潔。這就是函數式程序設計威力的關鍵——它允許了大幅改進的模塊化設計。這也正是函數式程序員必須追求的目標——更小、更簡潔、更通用的模塊，用我們將要描述的新黏合劑黏合起來。

3.把函數粘起來

兩種黏合劑中的第一種，使簡單的函數可以聚合起來形成複雜的函數。以一個簡單的處理問題來說明：將列表中的元素累加起來。我們用下面的語句定義列表：

listof X :: = nil | cons X (listof X)

這說明，一個元素類型爲X的列表（不論X是什麼），或是nil，代表一個沒有元素的空列表，或是一個X與另一個X的列表的cons。cons代表一個列表，其首元素爲X，而第二個以及後續元素即是另一個X的列表的元素。此處的X可以代表任何類型——例如，如果X是一個Integer（整數類型），那麼這個定義就是說，一個整數列表，或者是空的，或者是一個整數與另一個整數列表的cons。依照通常的實踐，我們寫列表時，只是簡單地將其元素包含在方括號裏，而不是將cons和nil顯式地寫出來。方便起見，這是一個簡單的速記法。例如：

[] 表示 nil
[1] 表示 cons 1 nil
[1 2 3] 表示 cons 1 ( cons 2 ( cons 3 nil ))

列表中的元素可以通過一個遞歸函數sum進行累加。sum必須爲兩類參數進行定義：一個空列表（nil），以及一個cons。由於沒有數字存在時，累加結果是0，因此我們定義：

sum nil = 0

又因爲cons的累加和可以通過將列表的第一個元素加到其餘元素的累加和上的方式進行計算，所以可以定義：

sum (cons num list) = num + sum list

檢查定義可以發現計算sum時，只有下面用紅色粗體標出的部分是特化的：

sum nil = 0

sum (cons num list) = num + sum list

這說明sum的計算可以通過一個通用的遞歸模式和特化的部分來模塊化。這個通用的遞歸模式習慣上被稱爲“遞減”（reduce），因此sum可以表達爲：

sum = reduce add 0

方便起見，reduce傳遞了一個二元函數add。add是這樣定義的：

add x y = x + y

只要將sum的定義參數化，我們便可以得到reduce的定義，即：

(reduce f x) nil = x
(reduce f x)(cons num list) = f num ((reduce f x) list)

這裏我們寫出了(reduce f x)兩邊的括號以強調它代替了sum。習慣上括號是省略的，因此 ((reduce f x) list)寫作(reduce f x list)。一個三元函數如reduce，當只提供兩個參數時，將成爲關於那個餘下參數的一元函數。一般地，對一個N元函數，提供了M(< N)個參數後，該函數便成爲了關於餘下的N-M個參數的函數。我們在下文中將遵守這一約定。

用這種方式將sum模塊化之後，我們就可以通過對這部分的重用來收穫福利了。最有趣的部分就是，reduce可以（直接）用於編寫一個函數來計算列表中元素的累乘積，而不需要更多的編程步驟：

product = reduce multiply 1

它也可以用來測試一個布爾值的列表中是否至少有一個元素爲真：

anytrue = reduce or false

或者它們是否都爲真：

alltrue = reduce and true

理解(reduce f a)的一種方式是，將其看作一個將列表中的所有cons替換爲f，將所有nil替換爲a的函數。以列表[1,2,3]爲例，既然它表示：

cons 1 (cons 2 (cons 3 nil))

那麼(reduce add 0)將其轉換爲：

add 1 (add 2 (add 3 0)) = 6

而(reduce multiply 1)將其轉換爲：

multiply 1 (mulitiply 2 (mulitiply 3 1)) = 6

於是，很明顯地，(reduce cons nil)將複製列表本身。既然將一個列表追加到另一個列表上的方式是將前一個列表的元素cons到後一個列表前部，我們便得到：

append a b = reduce cons b a

例如：

append [1,2] [3,4] = reduce cons [3,4] [1,2]
= (reduce cons [3,4]) (cons 1 ( cons 2 nil ))
= cons 1 ( cons 2 [3,4]))
= [1,2,3,4] （將cons替換爲cons，將nil替換爲[3,4]）

一個用於將列表中全部元素翻倍的函數可以寫作：

doubleall = reduce doubleandcons nil
doubleandcons num list = cons ( 2*num ) list

doubleandcons可以進一步模塊化，首先分解爲：

doubleandcons = fandcons double
double n = 2*n
fandcons f elem list = cons (f elem) list

繼續分解：

fandcons f = cons . f

其中“.”（函數複合，一個標準運算符）定義爲：

(f . g) h = f(g h)

爲證明fandcons的定義是正確的，我們代入一些參數：

fandcons f elem
= (cons . f) elem
= cons (f elem)

因此

fandcons f elem list = cons (f elem) list

最終得到的版本是：

doubleall = reduce (cons . double) nil

繼續模塊化，我們得到：

doubleall = map double
map f = reduce (cons . f) nil

其中map使任意的函數作用於列表的全部元素之上。map是另一個很通用的函數。

我們甚至可以寫出一個函數累加矩陣中的所有元素，該矩陣用列表的列表表示。這個函數是：

summatrix = sum . map sum

map sum使用函數sum分別計算所有行的元素之和，而後最左邊的sum將每一行的元素之和累加起來，從而得到整個矩陣的累加和。

這些例子應該已經足以使讀者確信，一點模塊化的努力可以產生很大的效果。通過將一個簡單的函數（sum）模塊化爲一個“高階函數”與一些簡單參數的聚合，我們得到了一個部件（reduce），它可以用於編寫與列表有關的許多函數，而又不再需要（更多的）編程努力。不止是對有關列表的函數可以這麼幹，舉另外一個例子，考慮數據類型“有序標記樹”，其定義是：

treeof X ::= node X (listof (treeof X))

這個定義表明，一棵X的樹，由一個標記類型爲X的結點（node），以及一個子樹列表組成，而這些子樹也是X的樹。例如，樹：

           1 o
            /\
           /  \
          /    \
        2 o     o 3
                |
                |
                |
                o 4

可以被表示成：

node 1(cons
  (node 2 nil)
  (cons (node 3
    (cons (node 4 nil) nil)
  )
nil))

我們不再給出一個函數例子並將它抽象爲高階函數，取而代之的是，直接給出一個類似於reduce的函數redtree。回憶一下，reduce有兩個參數，一個用於取代cons，另一個用於取代nil。既然樹由node，cons和nil組成，那麼redtree必須有三個參數——用於分別取代上述三者。由於樹和列表不是同一種類型，我們得定義兩個函數分別處理它們。因此我們定義：

redtree f g a (node label subtrees) = f label (redtree' f g a subtrees )
redtree' f g a (cons subtree rest) = g (redtree f g a subtree) (redtree' f g a rest)
redtree' f g a nil = a

［這相當於f取代node，g取代cons，a取代nil。］

很多有趣的函數都可以通過把redtree和其他函數粘起來的方法來定義。例如，要把一棵數字樹上的所有標記累加起來，可以使用：

sumtree = redtree add add 0

以我們剛纔表述的那棵樹爲例，sumtree展開成：

add 1
(add (add 2 0)
(add (add 3
(add (add 4 0) 0))
0))
= 10

要生成一個包含樹中全部標記的列表，可以用：

labels = redtree cons append nil

仍然是那個例子，得到：

cons 1
(append (cons 2 nil)
(append (cons 3
(append (cons 4 nil) nil))
nil))
= [1,2,3,4]

最後，可以定義一個類似於map的函數，此函數使函數f作用於樹中的全部標記上：

maptree f = redtree (node . f) cons nil

以上這些操作之所以可行，是因爲函數式語言允許將傳統型語言中不可分解的函數表達爲一些部件的聚合，也就是一個泛化的高階函數與一些特化函數的聚合。這樣的高階函數一旦定義，便使得很多操作都可以很容易地編寫出來。不論何時，只要一個新的數據類型被定義，就應當同時定義用於處理這種數據的高階函數。這樣就簡化了對數據類型的處理，同時也將與它的表示細節相關的知識局部化了。與函數式語言最相像的傳統程序語言是可擴展語言，只要有需求，這種程序語言就好像隨時都可以擴展出新的控制結構一樣。

4.把程序粘起來

函數式語言提供的另一種黏合劑使得所有程序都可以粘在一起。回憶一下，一個完整的函數式程序只不過是一個從輸入映射到輸出的函數。如果f和g是這樣的程序，那麼對程序(g.f)當提供了輸入參數input之後，得到：

g (f input)

程序f計算自身的輸出，此輸出被用作程序g的輸入。傳統上，這是通過將f的輸出儲存在臨時文件中實現的。這種方法的毛病是，臨時文件可能會佔用太大的空間，以至於將程序黏合起來變得很不現實。函數式語言提供了一種解決方案。程序f和g嚴格地同步運行，只有當g試圖讀取輸入時，f才啓動，並且只運行足夠的時間，恰好可以提供g需要讀取的輸出數據。而後f將被掛起，g將繼續執行，直到它試圖讀取另一個輸入。一個額外的好處是，如果g沒有讀取完f的全部輸出就終止了，那麼f也將被終止。f甚至可以是一個不會自行終止的程序，它可以產生無窮多的輸出，因爲當g運行結束時，f也將被強行終止。這就使得終止條件可以與循環體分離——一種強大的模塊化形式。

這種求值方式使得f儘可能地少運行，因此被稱爲“惰性求值（lazy evaluation）”。它使得將程序模塊化爲一個產生大量可能解的生成器與一個選取恰當解的選擇器的方案變得可行。有些其他的系統也允許程序以這種方式運行，但只有函數式語言對每一個函數調用都一律使用惰性求值，使得程序的每個部分都可以用這種方式模塊化。惰性求值也許是函數式程序員的拿手利器中威力最大的模塊化工具。

4.1.牛頓－拉夫森求根法

我們將編寫一些數值算法以展現惰性求值的威力。首先，考慮用於求解平方根的牛頓－拉夫森算法。該算法從一個初始的近似值a0開始計算數N的平方根，爲了求得更好的解，它使用下述規則：

a(n+1) = (a(n) + N/a(n)) / 2

如果近似值序列趨近於某一個極限a，那麼

a = (a + N/a) / 2
2a = a + N/a
a = N/a
a*a = N
a = squareroot(N)

事實上，這個近似值序列確實迅速地趨近於一個極限。平方根算法取一個允許誤差eps爲參數，當兩個相鄰的近似值之差的絕對值小於eps時，算法便終止了。

這個算法通常被編寫爲類似下面這樣：

C N IS CALLED ZN HERE SO THAT IT HAS THE RIGHT TYPE
X = A0
Y = A0 + 2.*EPS
C THE VALUE OF Y DOES NOT MATTER SO LONG AS ABS(X-Y).GT.EPS
100 IF (ABS(X-Y).LE.EPS) GOTO 200
Y = X
X = (X + ZN/X) / 2
200 CONTINUE
C THE SQUARE ROOT OF ZN IS NOW IN X

［這是一段FORTRAN的程序，C代表註釋行。.LE.是“Less than or Equal to”（小於或等於）的縮寫，同理.GT.是“大於”的意思。]

在傳統型語言中，這個程序是不可分解的。我們將利用惰性求值將其化爲更加模塊化的形式，而後演示所生成部件的一些其他用途。

由於牛頓－拉夫森算法計算的是一個近似值的序列，故將它寫作一個使用近似值列表的程序就再自然不過了。每個近似值都可以通過下面的函數從前一個值計算得到：

next N x = (x + N/x) / 2

因此(next N)是從一個近似值映射到下一個值的函數。調用函數f，得到近似值序列：

[a0, f a0, f(f a0), f(f(f a0)), ...]

我們可以定義一個函數來計算：

repeat f a = cons a (repeat f (f a))

因此近似值序列可以這樣計算：

repeat (next N) a0

repeat是一個具有“無窮”輸出的函數的例子——但這沒關係，因爲超出程序其餘部分需求的近似值並不會被計算。無窮性只是潛在的：它只說明，只要有需求，就可以計算出任意數量的近似值，repeat本身不會強加任何限制。

求根函數的剩餘部分是函數within，它取一個允許誤差與一個近似值列表作爲參數，並在列表中查找差值不超過允許誤差的一對相鄰的近似值。這個函數可以定義爲：

within eps (cons a (cons b rest)) = {
= b, 如果 abs(a-b) <= eps
= within eps (cons b rest), 其他情況
}

將這兩個部件結合起來，

sqrt a0 eps N = within eps (repeat (next N) a0)

現在我們得到了求根函數的兩大部件，便可以嘗試用不同的方式組合它們。將要進行的修改之一，是將判斷條件改爲“相鄰近似值的比趨近1”而不是“差趨近0”。這對於非常小的數字而言更加合適（當初始的相鄰近似值之間的差值很小時），對非常大的數字也是如此（當舍尾產生的誤差比允許誤差大很多時）。我們只需要定義一個函數來替換within，而並不需要改寫生成近似值的部件：

relative eps (cons a (cons b rest)) =
= b, 如果 abs(a-b) <= eps*abs b
= relative eps (cons b rest), 其他情況

［注意：relative裏的eps與within裏的eps定義是不同的！前者是絕對誤差後者是相對誤差！］

4.2.數值微分

我們已經重用了平方根近似值序列，當然，對函數within和relative的重用也是可能的，它們能夠與任何一個生成近似值序列的數值算法配合。我們將這樣來編寫數值微分算法。

函數在某一點的微分，便是其圖象在該點的斜率。通過分別計算函數在該點與一個臨近點處的取值，而後計算兩點連線斜率的方法，可以很容易地估計出微分的值。這基於一個假定：如果這兩點靠得足夠近，那麼函數圖象在兩點之間不會彎曲得很厲害。於是有下述定義：

easydiff f x h = (f(x+h)-f x) / h

爲了得到良好的近似值，h應該很小。不幸的是，如果h太小，那麼f(x+h)與f(x)會相當接近，因此在相減過程中產生的舍尾誤差可能會掩蓋了計算結果。如何爲h選取恰當的值呢？解決這個矛盾一種合理的方案是：從一個較大取值開始，不斷減小h的值，並求出一個近似值序列。這個序列將趨近於該點的導數，但最終會由於舍尾誤差的存在而不可救藥地變得不精確。如果我們用(within eps)來選取第一個足夠精確的近似值，那麼舍尾誤差影響結果的風險將會大大降低。我們需要一個函數來計算這個序列：

differentiate h0 f x = map (easydiff f x) (repeat halve h0)
halve x = x/2

此處h0是h的初值，而後繼取值是通過不斷減半得到的。通過這個函數，任意點處的導數可以這樣計算：

within eps (differentiate h0 f x)

但是，甚至這個方案也不是那麼令人滿意的，因爲近似值序列收斂得相當慢。解決這個問題需要一點數學知識，序列中的元素可以記爲：

微分的精確值 ＋ 一個關於h的誤差項

理論表明，該誤差項與h的某一次冪大致成正比，因此當h減小時，誤差也會減小。設精確值爲A，而誤差項爲B*h**n [**是求冪運算符］。由於計算每個近似值時所用的h取值是下一個的兩倍，故任意兩個連續的近似值可以表示成：

a(i)   = A + B*(2**n)*(h**n)
a(i+1) = A + B*(h**n)

現在就可以消去誤差項了，我們得到：

A=(a(i+1)*(2**n) - a(i))/(2**n - 1)

當然，誤差項只不過“大致”與h的某一次冪（成正比），因此這個結論也是近似的。但這是一個好得多的近似。這一改進可以通過下述函數作用於所有相鄰的近似值對之上：

elimerror n (cons a (cons b rest)) =
= cons ((b*(2**n)-a)/(2**n-1)) (elimerror n (cons b rest))

從一個近似值序列中消除誤差項的操作產生了另一個收斂速度快得多的序列。

使用elimerror之前還有一個問題需要解決——我們必須知道n的正確值。通常這個值很難預測，但卻很容易衡量。不難驗證，下述函數能夠正確地消除誤差項，但在此我們並不給出證明。

order (cons a (cons b (cons c rest))) =
= round(log2( (a-c)/(b-c) - 1 ))
round x = 最接近x的整數
log2 x  = x以2爲底的對數

現在，一個通用的近似值序列優化函數可以定義爲：

improve s = elimerror (order s) s

使用improve能夠更加高效地計算函數f的導數，如下：

within eps (improve (differentiate h0 f x))

improve只對利用一個不斷減半的參數h計算得到的近似值序列適用。但是，如果improve作用於這樣的序列，那麼其結果也是一個這樣的序列！這意味着一個近似值序列可以優化不止一次。每一次優化的過程中，都有一個不同的誤差項被消除，因此優化產生的序列收斂得越來越快。因此，可以非常高效地計算導數：

within eps (improve (improve (improve (differentiate h0 f x))

從數值分析的角度講，這似乎是一個“第四階方法”(fourth order method)，可以迅速地給出準確的結果。甚至可以定義：

super s = map second (repeat improve s)
second (cons a (cons b rest)) = b

super函數使用repeat improve來生成一個不斷被優化的近似值的序列的序列。［就是說，生成一個序列，其中每一個元素是一個近似值序列，而這個元素是用前一個元素優化得到的。］同時，super提取出每個近似值序列中的第二個元素，構造出一個新的序列（已經確認，第二元素是最佳選擇——它比首元更精確，而且不需要額外的計算）。這個算法的確非常複雜——更多的近似值被計算的同時，它使用了不斷優化的數值方法。可以用下面的程序非常非常高效地計算導數：

within eps (super (differentiate h0 f x))

這個案例可能就像是用大錘敲碎堅果一樣（大材小用），但關鍵是，甚至一個像super一樣複雜的函數，當被惰性求值的方法模塊化時，也會變得很容易表達。

4.3.數值積分

在這一部分我們將討論的最後一個例子是數值積分。問題的描述很簡單：給出一個返回實數，並有一元實數參數的函數，以及兩個端點a和b，估算兩點之間曲線f下方的面積。估算面積的最簡單方法是假定f趨近於直線，此時面積就是：

easyintegrate f a b = (f a + f b)*(b-a)/2

不幸的是，除非a與b足夠接近，否則這個估算似乎非常不精確。更好的估算方法是，將a與b之間的區間分爲兩段，分別估算子區間上的面積，再將結果加起來。我們可以定義一個不斷趨近於準確值的積分近似值序列，首先使用上述方程進行第一次近似，而後將分別趨近於兩個子區間上的子積分準確值的（兩個）近似值累加起來以得到新的（積分總體的）近似值。計算這個序列可以使用函數：

intergrate f a b = cons (easyintergrate f a b)
(map addpair (zip (intergrate f a mid)
(intergrate f mid b)))
式中 mid = (a+b)/2

zip是另一個標準的表處理函數。它讀取兩個列表，並返回一個有序對的列表，每個有序對由兩個輸入列表中對應的元素組成。從而第一對由列表一和列表二的首元組成，第二對由列表一和列表二的第二個元素組成，以此類推。zip可以定義爲：

zip (cons a s) (cons b t) = cons (pair a b) (zip s t)

在函數intergrate中，zip用於生成由兩個子區間上相對應的積分近似值對組成的列表，而map addpair用於將有序對中的元素相加，從而生成一個原積分的近似值列表。

實際上，這個版本的intergrate函數相當低效，因爲它持續不斷地重複計算f的值。就像所寫的一樣，easyintergrate計算了f在a和b兩處的值，而對intergrate的遞歸調用將重複計算它們。同樣的，(f mid)也在遞歸調用中重複計算了。因此，更可取的是下述從不重複計算f的版本：

intergrate f a b = interg f a b (f a) (f b)
integ f a b fa fb = cons ((fa+fb)*(b-a)/2)
(map addpair (zip (interg f a m fa fm)
(interg f m b fm fb)))
式中 m = (a+b)/2
fm = f m

integrate給出了一個不斷趨近準確值的積分近似值列表，正如differentiate在上一小節中所做的一樣。因此可以寫出計算式以求出所需任意精度的積分值，如下：

within eps (intergrate f a b)
relative eps (integrate f a b)

這個積分算法與上一小節中的第一個微分算法有着同樣的缺點——它收斂得相當慢。序列中的第一個近似值僅僅用了兩個相距(a-b)的點來計算（通過easyintergrate）。第二個近似值也（除了a、b之外）用到了中點，因此相鄰兩點之間的間距僅爲(b-a)/2。第三個近似值在兩個子區間上作同樣的處理，因此間距僅爲(b-a)/4。很清楚，每個近似值對應的相鄰兩點之間的間距在計算下一個值時被減半了。將這一間距看作h，那麼這個序列就可以成爲上一小節中定義的improve函數的優化對象了。因此我們可以寫出（函數來計算）快速收斂的積分近似值序列，例如：

super (intergrate sin 0 4)
improve (intergrate f 0 1)
式中 f x = 1/(1+x*x)

（後一個序列是用於計算pi/4的“第八階方法”。其中的第二個近似值只需要計算5次f的取值，但卻具有5位準確數字。）

在本節中我們選取了一些數值算法並將它們函數化地編寫出來，把惰性求值當做了黏合部件的黏合劑。由於惰性求值的存在，使得我們可以用很多新的方式來模塊化這些算法，從而產生用途廣泛的函數，例如within，relative和improve。通過這些部件的不同組合，我們簡單而明瞭地編寫出了一些相當不錯的數值算法。

5.人工智能中的例子

我們已經指出，函數式語言威力強大主要是因爲它們提供了兩種新的黏合劑：高階函數和惰性求值。在本節中，我們將討論人工智能中一個大一點的實例，並演示如何使用這兩種黏合劑來十分簡單地編寫它。

我們選取的實例是alpha-beta“啓發式搜索”，一個用於估計遊戲者所處形勢好壞的算法。該算法預測遊戲局勢的可能發展，但會避免對無意義局勢的進一步探究。

令遊戲局勢使用position類型的對象來表示。這個類型依據遊戲的不同而不同，我們不對此作任何假定。必然有一種方法可以知曉對某一個局勢能夠採取的行動：假定有一個函數：

moves: position -> listof position

該函數以一個遊戲局勢爲參數，並返回一個可以由自變量出發，通過一步行動而形成的position的列表。以noughts and crosses遊戲（tic-tac-toe）爲例：

這個函數假定通過當前局勢總是可以判定現在是哪位遊戲者的回合。在noughts and crosses中，可以通過數出0與X的數目來做到這一點。在類似於象棋的遊戲中，可能必須在position類型中顯式包含這一信息。

利用函數moves，第一步是構造一棵博弈樹。這棵樹的結點都用局勢來標記，而一個結點的子結點用從該結點一步便可到達的局勢標記。也就是說，如果一個結點標記爲局勢p，那麼它的子結點將使用(moves p)中的局勢來標記。一棵博弈樹完全有可能是無窮的，如果這個遊戲可以在雙方都不勝的情形下永遠進行下去的話。博弈樹與第2節中討論的樹完全類似——每個結點都有一個標記（它所代表的局勢）與一個子結點列表。因此我們可以使用相同的數據類型來表示它們。

博弈樹是通過反覆運用moves而構造出來的。構造從根局勢開始，moves用於生成根結點處子樹的標記，而後moves被用於生成子樹的子樹，依此類推。這一遞歸模式可以用一個高階函數表示：

reptree f a = node a (map (reptree f) (f a))

使用這個函數可以定義另一個函數，該函數從一個特定的局勢開始生成博弈樹：

gametree p = reptree moves p

例如圖1所示。此處使用的高階函數reptree與上一節中用於構造無窮列表的函數repeat是類似的。

圖1：一棵博弈樹的實例

alpha-beta算法從一個給定的局勢出發，就遊戲的發展將會是有利還是不利作出判斷。然而，要做到這一點，它必須能夠在不考慮下一步的情況下粗略地估計某一個局勢的“價值”。在後繼局勢不可預測時必須使用這一函數，它也可以用來對算法進行先期引導。靜態估價的結果是從計算機的角度考慮的，是對該局勢的前途的度量（假設在遊戲中計算機與人對抗）。結果越大，局勢對計算機而言越好。結果越小，局勢越糟。最簡單的此類函數將會，比如說，對計算機確定勝利的局勢返回+1，對計算機確定失敗的局勢返回-1，而對其它的局勢返回0。在現實中，靜態估價函數會衡量各種使局勢“看上去不錯”的因素。例如，具體的好處，以及象棋中對中心的控制。假定有這樣一個函數：

static: position -> number

既然一棵博弈樹是一個(treeof position)，那麼它就可以被函數(maptree static)轉換爲一個(treeof number)，該函數對樹中所有的（也許是無窮多個）局勢進行靜態估價。此處使用了第2節中定義的函數maptree。

給出一棵靜態估價樹之後，其中各個局勢的真值究竟是多大？特別地，對根局勢應該賦予什麼值？不是它的靜態值，因爲那只是一個粗略的猜測。一個結點被賦予的值，必須由其子結點的真值決定。這一過程的完成，基於每個遊戲者都會選擇對自己最有利的行動的假定。回憶一下，高值意味着計算機的有利形勢。很明顯，當計算機從任意的局勢開始下一步行動時，它將選擇通往真值最高的子結點的行動。類似地，對手將會選擇通往真值最低的子結點的行動。假定計算機與其對手輪流行動，那麼當輪到計算機行動時，節點的真值用函數maximise計算，反之用minimise計算。

［所謂“真值”（true value），可能是我翻譯得不好，此處理解爲類似“真正的價值”的意思吧，是一個量度，不是邏輯學裏的0和1哦。］

maximise (node n sub) = max (map minimise sub)
minimise (node n sub) = min (map maximise sub)

此處max和min是關於列表的函數，分別返回列表中元素的最大值與最小值。上述定義是不完整的，因爲它們將永遠遞歸下去——沒有給出邊界情形。我們必須定義沒有後繼的結點的值（其標記）。因此靜態估價用於任一遊戲者勝利或者後繼局勢不可預測的情況下。maximise與minimise的完整定義是：

maximise (node n nil) = n
maximise (node n sub) = max (map minimise sub)
maximise (node n nil) = n
maximise (node n sub) = min (map minimise sub)

在這個階段，幾乎已經可以寫出一個取一個局勢作爲參數並返回其真值的函數了。可能是：

evaluate = maximise . maptree static . gametree

這個定義有兩個問題。首先，它不適用於無窮樹。maximise不斷地遞歸直到找到一個沒有子樹的結點——樹的端點。如果沒有端點那麼maximise就不會返回結果。第二個問題與第一個有關——甚至有窮的博弈樹（如noughts and crosses裏的那棵）事實上也可能相當大。估價整棵博弈樹是不現實的——搜索必須被限定在接下去的幾步之內。爲此可以將樹剪至一個固定的深度：

prune 0 (node a x) = node a nil
prune n (node a x) = node a (map (prune (n-1)) x)

(prune n)取一棵樹作爲參數並“剪去”與根結點的距離超過n的所有結點。如果一棵博弈樹被剪枝，那麼將強制maximise對深度爲n的結點執行靜態估價而不是進一步遞歸。因此evaluate可以被定義爲：

evaluate = maximise . maptree static . prune 5 . gametree

這將考慮其後（比如說）5步的形勢。

在此開發過程中我們已經使用了高階函數與惰性求值。高階函數reptree和maptree使得我們能夠很容易地構造與處理博弈樹。更重要的是，惰性求值確保了我們可以使用這種方式模塊化evaluate。由於博弈樹具有潛在的無窮結果，在沒有惰性求值的情況下，程序將永遠不會終止。我們將不能寫：

prune 5 . gametree

而不得不將這兩個函數整合成一個只構造樹的前五層的函數。更糟糕的是，甚至那前五層都可能已經太大以至於無法在同一時間內存儲於內存中。而在我們所寫的程序中，函數

maptree static . prune 5 . gametree

只是構造出了樹中maximise所需的部分。由於每一部分都可以在被maximise處理完之後丟棄（被垃圾收集器回收），故完整的樹從來沒有存儲於內存中。只有樹的一小部分在某一段時間內被儲存着。因此這個惰性程序很有效率。這一效率取決於maximise（組合鏈上的最後一個函數）與gametree（第一個函數）的相互作用，因此在沒有惰性求值的情況下，要完成任務，只能將組合鏈上的所有函數整合成一個大函數。這是對模塊化的強烈破壞，但也是通常的做法。通過單獨修補每個部件，我們就可以優化估價算法——這相對簡單。而一個傳統型程序員必須把整個程序作爲一個單元來修改，這就困難多了。

到目前爲止，我們只是描述了簡單的對最大最小值的處理（minimaxing）。但alpha-beta算法的核心是“計算maximise與minimise的值時常常不需要考慮整棵樹”這一觀察結果。考慮樹：

          max
          / \
         /   \
        /     \
       /       \
     min       min
     / \       / \
    /   \     /   \
   1     2   0     ?

相當奇怪地，爲了估價這棵樹，並不需要知道問號處的值。左子樹的最小值是1，但右子樹的最小值顯然是一個小於或等於0的值。因此這兩個最小值的最大值必然是1。這一觀察結果可以被泛化並內建到maximise和minimise之中。

第一步是將maximise拆分成max對一個數字列表的作用。也就是，將maximise分解爲：

maximise = max . maximise'

（minimise可以用類似的方法分解。由於maximise和minimise是完全對稱的，故我們將只討論maximise，而假定minimise也照此處理。）一旦這樣分解之後，maximise可以使用minimise'來發現minimise將對哪些數字求最小值，並且不再使用minimise本身。而後便可以在不查看某些數字的情況下便將它們丟棄。由於惰性求值的存在，如果maxmise並不會查看所有的數字列表，那麼一部分列表將不會被計算，這是對計算機時間的潛在節約。

將max從maximise中“約分出來”是很簡單的，得到：

maximise' (node n nil) = cons n nil
maximise' (node n l) = map minimise l
= map (min . minimise') l
= map min (map minimise' l)
= mapmin (map minimise' l)
式中 mapmin = map min

由於minimise' 返回一個數字列表，而這個列表的最小值是minimise的結果，故(map minimise' l)返回一個數字列表的列表。Maximise'應該返回這些列表中每個列表的最小值組成的列表，但只有其中［Maximise的返回值中］的最大值纔有用。我們應該定義一個mapmin的新版本以忽略那些最小值不重要的列表［在(map minimise' l)的返回值中］的最小值。

mapmin (cons nums rest) =
= cons (min nums) (omit (min nums) rest)

函數omit傳遞一個“潛在的最大值”——當前所發現的最小值中最大的一個——並忽略任何比該值小的最小值。

omit pot nil = nil
omit pot (cons nums rest) =
= omit pot rest, if minleq nums pot
= cons (min nums) (omit (min nums) rest), otherwise

minleq以一個數字列表和一個潛在最大值爲參數，如果列表的最小值小於或等於潛在最大值就返回真。要完成這一工作，它並不需要掃描整個列表！如果列表中有任意一個元素小於或等於潛在最大值，那麼列表的最小值肯定也是如此。該特別元素之後的所有元素都是無關緊要的——它們就像是上面例子中的問號一樣。因此minleq可以被定義爲：

minleq nil pot = false
minleq (cons num rest) port = true, if numn2

此處sort是多用途排序函數。現在估價函數定義爲：

evaluate = max . maximise' . highfirst . maptree static . prune 8 . gametree

也可能認爲，爲了限制搜索，只要考慮計算機或者對手的前三個最佳行動也已經足夠了。要編寫這樣的程序，只需要把highfirst換成(taketree 3 . highfirst)，其中：

taketree n = redtree (nodett n) cons nil
nodett n label sub = node label (take n sub)

taketree將樹上所有的結點替換爲最多有n個子結點的結點，它使用了函數(take n)，而該函數返回列表的前n個元素（如果列表比n短，那麼返回的元素就少一些）。

另一種優化是對剪枝的改良。上述程序甚至在局勢非常dynamic的情形下也會向前搜索固定的深度——（但是，）例如在國際象棋中，一旦皇后被威脅，也許就可以決定不再搜索了。通常可以定義某些“dynamic”的形勢，並在遇到這樣的結點之一時，不再繼續搜索而停止。假定有函數“dyramic”用以確定這樣的形勢，那麼只需要爲prune追加一個定義等式：

prune 0 (node pos sub) = node pos (map (prune 0) sub), if dynamic pos

在像這個程序一樣模塊化的程序裏，作出這樣的改動是很簡單的。如前所述，這個程序的效率，關鍵是由鏈中的最後一個函數maximise與第一個函數gametree的相互作用決定的，因此若沒有惰性求值，就只能寫成一個單一的程序。這樣的程序難於編寫，難於修改，而且，非常難於理解。

6.結論

在本文中，我們指出模塊化是成功的程序設計的關鍵。以提高生產力爲目標的程序語言，必須良好地支持模塊化程序設計。但是，新的作用域規則和分塊編譯的技巧是不夠的——“模塊化”不僅僅意味着“模塊”。我們分解程序的能力直接取決於將解決方案粘在一起的能力。爲了協助模塊化程序設計，程序語言必須提供優良的黏合劑。函數式程序語言提供了兩種新的黏合劑——高階函數與惰性求值。利用這些黏合劑可以將程序用新的、令人激動的方式模塊化，對此我們舉出了很多實例。越小、越通用的模塊越可能被廣泛地重用，使後續的程序設計工作變得簡單。這解釋了爲什麼函數式程序與傳統型程序比較，要小得多，也容易編寫得多。它也爲函數式程序員提供了一個追求目標。如果程序的任何部分是雜亂或者複雜的，那麼程序員就應當嘗試將其模塊化並泛化其部件。他應當期望把高階函數和惰性求值用作他做此事的工具。

當然，我們並不是指出高階函數與惰性求值的力與美的第一人。例如，Turner展示了這兩者如何在一個生成化學結構的程序裏大顯身手［Tur81］。Abelson和Sussman強調“流”（惰性列表）是構架程序的強大工具［AS86］。Henderson使用了流來構架函數式操作系統［P.H82］。本論文的主要貢獻是，斷言了模塊化自身，便是函數式語言強大威力的關鍵。

這與當前有關惰性求值的論戰也有關聯。有些人認爲函數式語言應當是惰性的，而其他人認爲不是這樣。有些人走折衷路線，只提供惰性列表以及用於構造它們的特殊語法（例如，在SCHEME中［AS86］）。本論文提供了更進一步的證據，證明惰性求值非常重要以至於不能被降爲二等公民。這也許是函數式程序員所擁有的最強大的黏合劑。人們不應當阻礙對這樣一個極爲重要的工具的使用。

致謝

在牛津程序設計研究組與Phil Wadler和Richard Bird的多次交談對本論文的寫作幫助甚大。約特堡查麥茲大學的Magnus Bondesson指出了一個數值算法的早期版本中的嚴重錯誤，同時也協助了很多其他算法的開發。本論文在英國科學與工程研究評議會提供的研究基金贊助下發表。

參考文獻

[AS86] H.Abelson,G.J.Sussman. 計算機程序的構造與解釋. 麻省理工學院出版社,波士頓,1986
[Hug89] J.Hughes. 函數式程序設計爲什麼至關重要. 計算機月刊,32(2),1989
[Hug90] John Hughes. 函數式程序設計爲什麼至關重要. D.Turner主編,函數式編程的研究主題. Addison Wesley,1990
[MTH90] R.Milner,M.Tofte,R.Harper. Standard ML的定義. 麻省理工學院出版社,1990
[oD80] 美利堅合衆國國防部. 程序語言Ada參考手冊. Springer-Verlag,1980
[P.H82] P.Henderson. 純函數式操作系統. 1982
[Tur81] D.A.Turner. 應用語言在語義上的優雅性. 1981年度函數式語言與計算機架構會議會報,海邊溫特渥,普茨茅斯,新漢普夏郡,1981
[Tur85] D.A.Turner. Miranda: 擁有多態類型的非嚴格語言. 1985年度函數式語言與計算機架構會議會報,1-16頁,南錫,法國,1985
[Wir82] N.Wirth. Modula-II程序設計. Springer-Verlag,1982

上次修改時間 2017-05-22

摘要